The Dynamic IS Curve when there is both Investment and Savings

The interest rate channel is key to the transmission of monetary policy, yet whether it is properly captured in baseline models of aggregate demand has been widely debated in recent years. In baseline models, the dependence of aggregate demand on interest rates is captured by the Euler equation, which originates in households' desire to substitute consumption across periods. The Euler equation improves on the static IS curve of IS-LM by being a dynamic IS curve, capturing the dependence of aggregate demand on all future interest rates, not just the current one. But the precise dependence it assigns seems unrealistic. Because it puts the same weight on all interest rates, the Euler equation puts an unrealistically high weight on future interest rates. This leads to the forward-guidance puzzle (Del Negro, Giannoni, and Patterson, 2012; Carlstrom, Fuerst, and Paustian, 2015), and questions the realism of the Euler equation in capturing the intertemporal dimension of the IS curve.

The recent literature on aggregate demand has considered several assumptions on the modeling of households' consumption—such as heterogeneity or bounded rationality—that can add discounting to the dynamic IS curve (i.e. the effect of interest rate cuts is weaker, the higher the horizon of the interest rate cut). While such models often show that intertemporal substitution is then only the first step in a transmission channel that goes through several amplification mechanisms, they retain the underlying assumption that the interest rate channel originates in (at least some) households' desire to intertemporally substitute consumption.

What interest rates have an initial lever on, however, is not only households' consumption, but also—perhaps primarily—firms' investment. In order to capture the dependence of aggregate demand on future interest rates, considering the dynamic IS curve in a model where the interest rate channel originates in both the savings decisions of households and the investment decisions of firms—like in the original Investment-Savings curve of IS-LM—can be better suited.

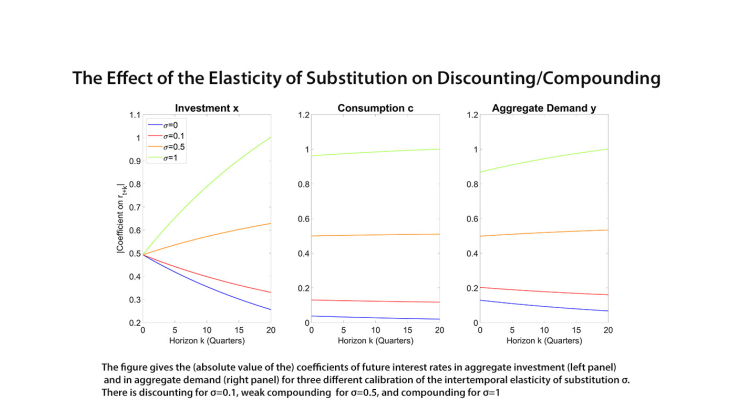
This paper derives an analytical expression of the dynamic IS curve in a model with both consumption and investment, capturing both the savings and the investment components of the interest rate channel. It shows that the weight on future interest rates in the generalized dynamic IS curve is shaped by several new factors absent in the simple IS curve that abstracts from the investment component. In particular, a key determinant of the extent of discounting in aggregate demand is then the intertemporal elasticity of substitution in consumption (IES). For a low IES—below 0.3 in the main calibration I use—interest rates are discounted in the dynamic IS curve, while for a higher IES they are instead compounded (i.e. the effect of interest rate cuts is stronger, the higher the horizon of the interest rate). Intuitively, this is because the IES determines the relative importance of the two components of the interest rate channel, and the one that originates in investment demand discounts future interest rates more heavily than the one that originates in intertemporal substitution.